[latexpage]
Let’s start off this section by examining the equation:
$(x-3)^2-(y-3)^2=4$
From the previous section, we recognize this equation as a circle with an origin located at (3,3). Wouldn’t it be nice to be able to shift the origin of the circle 3 units in the x direction and 3 units in the y direction so that it is smack dab in the middle of our curve? This would reduce the equation in
question to:
$(x)^2-(y)^2=4$
It’s obvious, though, that if we shift the origin, it will affect the coefficients of the equation due to its dependency on the natural axis. However, if we hold true to maintaining the integrity of the shape and simply just move to a different set of axis, we not only simplify the equation, but have prescribed methods of analysis that will help us achieve our answer much more efficiently.
The two methods to be discussed in this section are Translation of Axes and Rotation of Axis.
Simplification by Translation
The following variables will be used to illustrate the affects on a point when the origin is shifted from (0,0) to an arbitrary origin of (h,k).
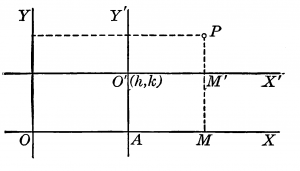In this illustration, ${\normalsubformula{\text{OX}}}$ and ${\normalsubformula{\text{OY}}}$ are the original set of axes. The coordinates (h,k) is the new location for the origin, denoted ${{O}^{‘}}$, which becomes the center point for the new axes ${{O}^{‘}{X}^{‘}}$ and ${{O}^{‘}{Y}^{‘}}$. Point P is ${\left(x,y\right)}$ in the original axes and ${\left({x}^{‘},{y}^{‘}\right)}$ in the new set of axes.
With that, we can develop some relationships:
\begin{equation*}
{x=\normalsubformula{\text{OA}}+\normalsubformula{\text{AM}}={x}^{‘}+h}
\end{equation*}
\begin{equation*}
{y=A{O}^{‘}+{M}^{‘}P={y}^{‘}+k}
\end{equation*}
With these relationships, when faced with an equation of a curve referenced to a specific axes, we can now refer to another pair of axes running through an origin (h,k) by simply plugging in $x’+h$ and $y’+k$ for x and y respectively. Once we run through the process of developing the new equivalent equation, we can drop the prime from the x and y variables and solve it as we would any other problem.
Let’s run through an example to further illustrate:
Example
Given the equation:
\begin{equation*}
{4x^{{2}}-6\normalsubformula{\text{xy}}+2y^{{2}}+\text{10}x-6y-\text{10}=0}
\end{equation*}
Let’s shift the origin to (h,k):
\begin{equation*}
\begin{matrix}{4({x}^{‘}+h)^{{2}}-6({x}^{‘}+h)({y}^{‘}+k)+2({y}^{‘}+k)^{{2}}+\text{10}({x}^{‘}+h)}\hfill\null
\\-6({y}^{‘}+k)-\text{10}=0\hfill\null \end{matrix}\hfill
\end{equation*}
Or:
\begin{equation*}
\begin{matrix}{4{x}^{{2}}-6{x}^{‘}{y}^{‘}+2{y}^{{2}}+(8h-6k+\text{10}){x}^{‘}+(-6h+4k-6){y}^{‘}}\hfill\null
\\+4h^{{2}}-6\normalsubformula{\text{kh}}+2k^{{2}}+\text{10}h-6k-\text{10}\hfill\null \end{matrix}\hfill
\end{equation*}
As you can see, only the ${x’}$, ${y’}$, and constant terms rely on h and k. To simplify, we can determine h and k so that the coefficients of two of the terms above, say ${x’}$ and ${y’}$ terms, disappear. To do this, set the terms:
\begin{equation*}
{8h-6k+\text{10}=0}
\end{equation*}
And
\begin{equation*}
{-6h+4k-6=0}
\end{equation*}
Two equations, two unknowns; solving them we get:
\begin{equation*}
{h=1}
\end{equation*}
\begin{equation*}
{k=3}
\end{equation*}
Plugging in h and k and simplifying, the translated equation is:
$4x^2-6xy+2y^2=14$ located at the coordinates (1,3)
Often times, we will encounter an equation to the second degree that has an ${x^{{2}}}$ and ${y^{{2}}}$ term but no xy term. The equation will resemble the form:
\begin{equation*}
{\normalsubformula{\text{Ax}}^{{2}}+\normalsubformula{\text{By}}^{{2}}+\normalsubformula{\text{Cx}}+\normalsubformula{\text{Dy}}+E=0}
\end{equation*}
With an equation of this form, we are granted an opportunity to translate and simplify in a more streamline manner than the one explained above.
Example
Given the equation:
\begin{equation*}
{4x^{{2}}-\text{12}y^{{2}}-\text{32}x-\text{24}y=1}
\end{equation*}
We can simplify this equation quickly by first gathering the x and y terms and rewriting such that the form looks like:
\begin{equation*}
{4\left(x^{{2}}-8x\right)-\text{12}\left(y^{{2}}+2y\right)=1}
\end{equation*}
And further:
\begin{equation*}
{4\left(x-4\right)^{{2}}-\text{12}\left(y+1\right)^{{2}}=1+\text{64}-\text{12}=\text{53}}
\end{equation*}
At this point, we can see the desired location of the translated origin at (-4,1), which by substituting x+4 for x and y-1 for y, we come to the simplified translated equation:
\begin{equation*}
{4x^{{2}}-\text{12}y^{{2}}=\text{53}}
\end{equation*}
Simplification by Rotation of Axes
Let’s say again we encounter an equation with the form:
\begin{equation*}
{\normalsubformula{\text{Ax}}^{{2}}+2\normalsubformula{\text{Hxy}}+\normalsubformula{\text{By}}^{{2}}+\normalsubformula{\text{Cx}}+\normalsubformula{\text{Dy}}+E=0}
\end{equation*}
We can simplify this equation by means of rotating the given axes in a way to eliminate the term ${\normalsubformula{\text{Hxy}}}$
Before we go any further, let’s illustrate what rotating the axes will look like:
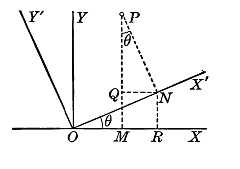In this illustration, ${\normalsubformula{\text{OX}}}$ and ${\normalsubformula{\text{OY}}}$ are the original set of axes with a point P located at (x,y). Rotating the axes ${\Theta }$ we get a new set of axes ${O{X}^{‘}}$ and ${O{Y}^{‘}}$ with the same point P now at ${\left({x}^{‘},{y}^{‘}\right)}$.
Setting these variables and establishing the dotted lines on the illustration above, we now can work out the following relations:
\begin{equation*}
{x={x}^{‘}\text{cos}(\Theta )-{y}^{‘}\text{sin}(\Theta )}
\end{equation*}
\begin{equation*}
{y={x}^{‘}\text{sin}(\Theta )+{y}^{‘}\text{cos}(\Theta )}
\end{equation*}
With these relationships, when given a complicated equation of a curve referenced to specific axes, we can now find a simplified equivalent referring to another pair of axes rotated at a given angle ${\Theta }$ running through the same origin. All we need to do is simply plug in ${{x}^{‘}\text{cos}(\Theta )-{y}^{‘}\text{sin}(\Theta )}$ and ${{x}^{‘}\text{sin}(\Theta )+{y}^{‘}\text{cos}(\Theta )}$ for x and y respectively.
Again, once we run through the process of developing the new equivalent equation, we can drop the prime from the x and y variables and solve it as we would any other problem.
Let’s run through a proof, take:
\begin{equation*}
{\normalsubformula{\text{Ax}}^{{2}}+2\normalsubformula{\text{Hxy}}+\normalsubformula{\text{By}}^{{2}}+\normalsubformula{\text{Cx}}+\normalsubformula{\text{Dy}}+E=0}
\end{equation*}
Substitute for x and y:
\begin{equation*}
\begin{matrix}{A({x}^{‘}\text{cos}(\Theta )-{y}^{‘}\text{sin}(\Theta ))^{{2}}+2H({x}^{‘}\text{cos}(\Theta
)-{y}^{‘}\text{sin}(\Theta ))({x}^{‘}\text{sin}(\Theta )}\hfill\null \\+{y}^{‘}\text{cos}(\Theta
))+B({x}^{‘}\text{sin}(\Theta )+{y}^{‘}\text{cos}(\Theta ))^{{2}}+C({x}^{‘}\text{cos}(\Theta )\hfill\null
\\-{y}^{‘}\text{sin}(\Theta ))+D({x}^{‘}\text{sin}(\Theta )+{y}^{‘}\text{cos}(\Theta )+E=0\hfill\null
\end{matrix}\hfill
\end{equation*}
Working out this equation can get long, so I will spare you the pain and move on to our next step. Since we are working to eliminate the xy term in the original equation, when you have the equation expanded, isolate the xy terms, which in this case would be:
\begin{equation*}
{-2A\text{sin}(\Theta )\text{cos}(\Theta )+2H\text{cos}^{{2}}(\Theta )-2H\text{sin}^{{2}}(\Theta )+2B\text{sin}(\Theta
)\text{cos}(\Theta )}
\end{equation*}
From trigonometry equivalents we know:
\begin{equation*}
{\text{cos}^{{2}}(\Theta )-\text{sin}^{{2}}(\Theta )=\text{cos}(2\Theta )}
\end{equation*}
And
\begin{equation*}
{2\text{sin}(\Theta )\text{cos}(\Theta )=\text{sin}(2\Theta )}
\end{equation*}
The xy terms can be simplified to:
\begin{equation*}
{-\left(A-B\right)\text{sin}(2\Theta )+2H\text{cos}(2\Theta )}
\end{equation*}
So since we want to completely rid the xy term from the original equation, set the above equal to zero:
\begin{equation*}
{-\left(A-B\right)\text{sin}(2\Theta )+2h\text{cos}(2\Theta )=0}
\end{equation*}
Rearrange the above equation to isolate the ${\Theta }$ term for solving:
\begin{equation*}
{\text{tan}(2\Theta )=\frac{2H}{A-B}}
\end{equation*}
Solving the equation above for ${\Theta }$ will give us the angle in which we need to rotate the axes to completely eliminate the xy term in the original equation.
Example
Using the Rotation of Axes, simplify the equation:
\begin{equation*}
{\text{73}x^{{2}}+\text{72}\normalsubformula{\text{xy}}+\text{52}y^{{2}}+\text{30}x-\text{40}y-\text{75}=0}
\end{equation*}
${A=\text{73}}$
${2H=\text{72}}$
${B=\text{52}}$
Determine ${\Theta }$ that will eliminate the xy term using:
${\text{tan}(2\Theta )=\frac{2H}{A-B}=\frac{\text{72}}{\text{73}-\text{52}}}$ $ $
\begin{equation*}
{\Theta =\text{37}{}^{\circ}}
\end{equation*}
\begin{equation*}
{x={x}^{‘}\text{cos}(\text{37})-{y}^{‘}\text{sin}(\text{37})=\text{.}8{x}^{‘}-\text{.}6{y}^{‘}}
\end{equation*}
\begin{equation*}
{y={x}^{‘}\text{sin}(\text{37})+{y}^{‘}\text{cos}(\text{37})=\text{.}6{x}^{‘}+\text{.}8{y}^{‘}}
\end{equation*}
Working these values in to the original equation and simplifying we get:
\begin{equation*}
{\text{100}x^{{2}}-\text{42}y^{{2}}-\text{50}y=\text{75}}
\end{equation*}
