Thank for visiting the EngineerInTrainingExam.com Practice Questions Page for the EIT Exam. I put this these problems together in an effort to help you prepare and get an idea of the types and structure of questions on the exam. For each question, choose the best answer from the four options given. After each question, you will be given a detailed description of how the answer was obtained, so don’t worry if you get it wrong.
Enter you name and email address in the slots given to gain Instant Access
There is no time limit, but it wouldn’t be a bad idea to time yourself just to see where you stand.
Good Luck!
Question 1 |
$$571$$ | |
$$213.3$$ | |
$$273.1$$ | |
$$621.7$$ |
 $$\\$$
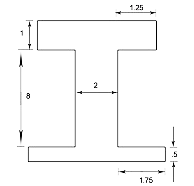
Determine A and \(\bar{y}\) for each shape:
\begin{matrix}
A_1=1(4.5) & A_2=8(2) & A_3=.5(5.5) \\
\bar{y_1}=.5+8+.5=9 & \bar{y_2}=.5+4=4.5 & \bar{y_2}=.25 \\
A_1\bar{y_1}=40.5 & A_2\bar{y_2}=72 & A_3\bar{y_3}=.69 \\
\end{matrix}\\
Plug in the values to determine} \(\bar{y}_{composite}\):
\begin{aligned}
\bar{y}_{composite}=\frac{\sum{A\bar{y}}}{\sum{A}}=\frac{40.5+72+.69}{4.5+16+2.75}=4.87
\end{aligned}
Determine the Centroidal Moment of Inertia for each shape and the distance from \(\bar{y}_{composite}\) for each shape noting that \( I_{rec}=\frac{bh^3}{12}\) :
\begin{matrix}
I_{c1}=\frac{4.5(1)^3}{12}=.375 & d_1=4.87-9=-4.13 \\
I_{c2}=\frac{2(8)^3}{12}=85.33 & d_2=.37 \\
I_{c3}=\frac{5.5(.5)^3}{12}=.057 & d_3=4.18 \\
\end{matrix}
Utilizing the Parallel Axis Theorem to get the Centroidal Moment of Inertia of the complete object we get:
\begin{aligned}
I=.375+4.5(-4.13)^2+85.33+16(.37)^2+.57+2.75(4.18)^2=213.3
\end{aligned}
$$\\$$
Determine A and \(\bar{y}\) for each shape:
\begin{matrix}
A_1=1(4.5) & A_2=8(2) & A_3=.5(5.5) \\
\bar{y_1}=.5+8+.5=9 & \bar{y_2}=.5+4=4.5 & \bar{y_2}=.25 \\
A_1\bar{y_1}=40.5 & A_2\bar{y_2}=72 & A_3\bar{y_3}=.69 \\
\end{matrix}\\
Plug in the values to determine} \(\bar{y}_{composite}\):
\begin{aligned}
\bar{y}_{composite}=\frac{\sum{A\bar{y}}}{\sum{A}}=\frac{40.5+72+.69}{4.5+16+2.75}=4.87
\end{aligned}
Determine the Centroidal Moment of Inertia for each shape and the distance from \(\bar{y}_{composite}\) for each shape noting that \( I_{rec}=\frac{bh^3}{12}\) :
\begin{matrix}
I_{c1}=\frac{4.5(1)^3}{12}=.375 & d_1=4.87-9=-4.13 \\
I_{c2}=\frac{2(8)^3}{12}=85.33 & d_2=.37 \\
I_{c3}=\frac{5.5(.5)^3}{12}=.057 & d_3=4.18 \\
\end{matrix}
Utilizing the Parallel Axis Theorem to get the Centroidal Moment of Inertia of the complete object we get:
\begin{aligned}
I=.375+4.5(-4.13)^2+85.33+16(.37)^2+.57+2.75(4.18)^2=213.3
\end{aligned}Question 2 |
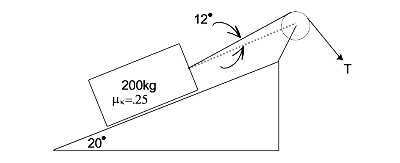
Cargo is being pulled up a ramp as shown in the figure below. The contents within are fragile so it's crucial the container is pulled up at a constant acceleration of \(3 \frac{m}{s^2}\). Determine the Tension necessary on the backside of the pulley (right side) to ensure the \(100kg\) contents are not disturbed.
$$T=903.4N$$ | |
$$T=1,155.9N$$ | |
$$T=671.1N$$ | |
$$T=853.2N$$ |
 $$\\$$
Using Newtons's Law, we know:
\begin{aligned}
&\sum F_x=ma_x \\
&\sum F_y=ma_y \\
&\sum F_y=ma_y=0 \;\;\;\;\text{where } a_y=0 \text{ so } \sum F_y=0 \\
&\sum F_y=0=N+Tsin(12)-Wcos(20) \\
\end{aligned}
\begin{equation} \label{eq:erl}
N=Wcos(20)-Tsin(12)
\end{equation}
\begin{aligned}
\sum F_x=ma_x \Rightarrow Tcos(12)+T-Wsin(20)-F_{\mu}=ma_x
\end{aligned}
Use Equation 1 to determine \(F_{\mu}\):
\begin{aligned}
F_{\mu}=\mu_{k}N=.25(Wcos(20)-Tsin(12))
\end{aligned}
Plugging this result in to \(\sum F_x\):
\begin{equation} \label{eq:er2}
Tcos(12)+T-Wsin(20)-.25(Wcos(20)-Tsin(12))=200kg(\frac{m}{s^2})
\end{equation}
We can now rearrange and solve for \(T\):
\begin{aligned}
T(1.98)-671N-461N+.052T=600N
\end{aligned}
ANSWER:
\begin{aligned}
T=853.2N
\end{aligned}
$$\\$$
Using Newtons's Law, we know:
\begin{aligned}
&\sum F_x=ma_x \\
&\sum F_y=ma_y \\
&\sum F_y=ma_y=0 \;\;\;\;\text{where } a_y=0 \text{ so } \sum F_y=0 \\
&\sum F_y=0=N+Tsin(12)-Wcos(20) \\
\end{aligned}
\begin{equation} \label{eq:erl}
N=Wcos(20)-Tsin(12)
\end{equation}
\begin{aligned}
\sum F_x=ma_x \Rightarrow Tcos(12)+T-Wsin(20)-F_{\mu}=ma_x
\end{aligned}
Use Equation 1 to determine \(F_{\mu}\):
\begin{aligned}
F_{\mu}=\mu_{k}N=.25(Wcos(20)-Tsin(12))
\end{aligned}
Plugging this result in to \(\sum F_x\):
\begin{equation} \label{eq:er2}
Tcos(12)+T-Wsin(20)-.25(Wcos(20)-Tsin(12))=200kg(\frac{m}{s^2})
\end{equation}
We can now rearrange and solve for \(T\):
\begin{aligned}
T(1.98)-671N-461N+.052T=600N
\end{aligned}
ANSWER:
\begin{aligned}
T=853.2N
\end{aligned}Question 3 |
$$y(t)=10+5e^{5t}$$ | |
$$y(t)=10+5e^{5t}$$ | |
$$y(t)=2-3e^{-5t}$$ | |
$$y(t)=2-3e^{5t}$$ |
Question 4 |
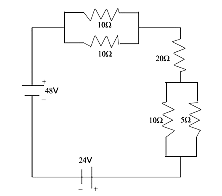
$$I=-.85\;amps$$ | |
$$I=2.1\;amps$$ | |
$$I=5.4\;amps$$ | |
$$I=-5.4\;amps$$ |
Question 5 |
$$x^2+(y+2)^2=7$$ | |
$$(x+2)^2+y^2=9$$ | |
$$x^2+(y+2)^2=9$$ | |
$$x^2+y^2=7$$ |
Question 6 |
A \(12V \) DC source has been running the circuit below for a long time. Given this information, determine the voltage across the Capacitor:
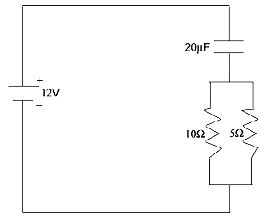
$$12\;V$$ | |
$$0\;V$$ | |
$$8.5\;V$$ | |
$$6\;V$$ |
Question 7 |
$$$900$$ | |
$$($12,900)$$ | |
$$($63.58)$$ | |
$$$13,100$$ |
Question 8 |
$$71.7\;MPa \sqrt{m}$$ | |
$$9.15\;MPa \sqrt{m}$$ | |
$$16.06\;MPa \sqrt{m}$$ | |
$$507.8\;MPa \sqrt{m}$$ |
Question 9 |
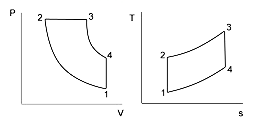
$$W_{cyc}=W_{23}+W_{34}-W_{12}$$ | |
$$W_{cyc}=Q_{23}+-Q_{41}$$ | |
$$\eta_t= \frac{W_{cyc}}{Q_{cyc}}$$ | |
$$Q_{cyc}=Q_{23}-Q_{41}$$ |
Question 10 |
$$1$$ | |
$$3$$ | |
$$0$$ | |
$$2$$ |
|
List |